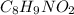Question

Crime scene investigators keep a wide variety of compounds on hand to help with identifying unknown substances they find in the course of their duties. one such investigator, while reorganizing their shelves, has mixed up several small vials and is unsure about the identity of a certain powder. elemental analysis of the compound reveals that it is 63.57% carbon, 6.000% hydrogen, 9.267% nitrogen, 21.17% oxygen by mass. which of the following compounds could the powder be?

Answer 1

The question is incomplete, here is the complete question:

Crime scene investigators keep a wide variety of compounds on hand to help with identifying unknown substances they find in the course of their duties. One such investigator, while reorganizing their shelves, has mixed up several small vials and is unsure about the identity of a certain powder. Elemental analysis of the compound reveals that it is 63.57% carbon, 6.000% hydrogen, 9.267% nitrogen, 21.17% oxygen by mass. Which of the following compounds could the powder be?

a.)
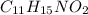`C_(11)H_(15)NO_2` = 3,4-methylenedioxymethamphetamine (MDMA), illicit drug

b.)
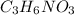`C_3H_6NO_3` = hexamethylene triperoxide diamine (HMTD), commonly used explosive

c.)
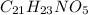`C_(21)H_(23)NO_5` = heroin, illicit drug

d.)
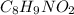`C_8H_9NO_2` = acetaminophen, analgesic

e.)
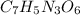`C_7H_5N_3O_6` = 2,4,6-trinitrotoluene (TNT), common used explosive

f.)
`C_(17)H_(19)NO_3` = morphine, analgesic

g.)
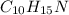`C_(10)H_(15)N` = methamphetamine, stimulant

h.)
`C_4H_5N_2O` = caffeine, stimulant

Answer: The powder could be acetaminophen, analgesic having chemical formula
`C_8H_9NO_2`

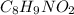
Step-by-step explanation:

We are given:

Percentage of C = 63.57 %

Percentage of H = 6.000 %

Percentage of N = 9.267 %

Percentage of O = 21.17 %

Let the mass of compound be 100 g. So, percentages given are taken as mass.

Mass of C = 63.57 g

Mass of H = 6.000 g

Mass of N = 9.267 g

Mass of O = 21.17 g

To formulate the empirical formula, we need to follow some steps:

• Step 1: Converting the given masses into moles.

Moles of Carbon =
`\frac{\text{Given mass of Carbon}}{\text{Molar mass of Carbon}}=(63.57g)/(12g/mole)=5.30moles`

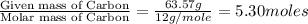
Moles of Hydrogen =
`\frac{\text{Given mass of Hydrogen}}{\text{Molar mass of Hydrogen}}=(6.000g)/(1g/mole)=6.000moles`

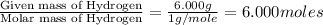
Moles of Nitrogen =
`\frac{\text{Given mass of nitrogen}}{\text{Molar mass of nitrogen}}=(9.267g)/(14g/mole)=0.662moles`

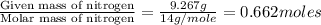
Moles of Oxygen =
`\frac{\text{Given mass of oxygen}}{\text{Molar mass of oxygen}}=(21.17g)/(16g/mole)=1.32moles`

• Step 2: Calculating the mole ratio of the given elements.

For the mole ratio, we divide each value of the moles by the smallest number of moles calculated which is 0.662 moles.

For Carbon =
`(5.30)/(0.662)=8`

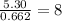
For Hydrogen =
`(6.00)/(0.662)=9.06\approx 9`

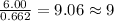
For Nitrogen =
`(0.662)/(0.662)=1`

For Oxygen =
`(1.32)/(0.662)=1.99\approx 2`

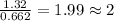
• Step 3: Taking the mole ratio as their subscripts.

The ratio of C : H : N : O = 8 : 9 : 1 : 2

The empirical formula for the given compound is
`C_8H_9NO_2`

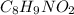
Hence, the powder could be acetaminophen, analgesic having chemical formula
`C_8H_9NO_2`

Answer 2

So 100 g of this substance has 63.57 g of carbon, 6 g of hydrogen, 9.267 of nitrogen, and 21.17 of oxygen. I need to have them all in moles (n). You can find the molar mass (M) of each element in a periodic table.

n = m/M
63.57 g C -> 63.57 g C/12.01 g/mol = 5.29 moles C
6 g H -> 6 g C/1.008 g/mol = 5.95 moles H
9.267 g N -> 9.267 g N/14.01 g/mol = 0.6615 moles N
21.17 g O -> 21.17/16.00 g/mol = 1.32 moles O

So the minimum formula has this rate:

C 5.29 H 5.95 N 0.6615 O 1.32

Now you should divide all those numbers by the smallest one (1.32):

C 4 H 4.5 N 0.5 0 1

Now it looks a lot more like a molecular formula… but we still have fractions.

Let’s multiply all numbers by 2:

C8H9N1O2

Now they are all whole numbers!

So the minimum formula is C8H9NO2

The minimum formula is not always equal to the molecular formula… but in this case, I found there is a molecular formula with this same numbers, and it’s called acetaminophen.