Answer:
Option C. 135 in³
Explanation:
Since volume is a three dimensional unit in which three dimensions of any object is multiplied.
If the sides of two similar pyramids are in the ratio of
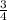 , ratio of their volume will be =
, ratio of their volume will be =
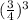
Which clearly says that
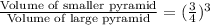
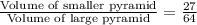
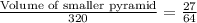
Volume of the smaller pyramid =
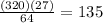
Therefore, volume of the smaller pyramid is 135 in³
Option C. 135 in³ is the correct answer.