Answer:
Equation has 1 real root and 2 complex roots.
Explanation:
Given :
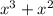 =
=
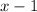 .
.
To find : Which statement describes the roots of this equation.
Solution : We have
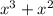 =
=
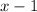 .
.
We can write it as
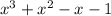 .
.
Graphs of both these functions shows one common point, this means that the equation
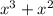 =
=
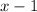 has one real solution (approximately, x≈-1.839).
has one real solution (approximately, x≈-1.839).
But degree is 3 .
So, it has maximum 3 root.
Therefore, Equation has 1 real root and 2 complex roots.