Question

The product of two consecutive negative integers is 600. What is the value of the lesser integer?

Answer 1

let's say the first number is -a, so "a" will be some positive value, and we multiply -1 to it, we get the -a

a consecutive number from it, is either, ahead or before it, so, -a + 1 or -a -1, is a consecutive integer, hmm let's use -a + 1 then

so, the two numbers are -a and -a + 1

we know their product is 600


`\bf (-a)(-a+1)=600\implies a^2-a=600 \\\\\\ \begin{array}{lcclll} a^2&-a&-600=0\\ &\uparrow &\uparrow \\ &-25+24&-25\cdot 24 \end{array} \implies (a-25)(a+24)=0 \\\\\\ \begin{cases} a-25=0\implies &\boxed{a=25}\\ a+24=0\implies &a=-24 \end{cases}`

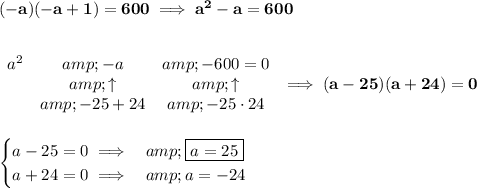
we use the positive one, because we're using -1 in front of the "a"

what's the lesser integer? well, what's -a+1? which one is lesser?

Answer 2

Lesser integer = -25

Explanation:

Let a be the lesser integer. Given that 2 numbers are consecutive integers.

Other integer = a + 1

The product of two consecutive negative integers is 600

So we have

a x ( a + 1 ) = 600

`a^2+a-600=0\\\\(a-24)(a+25)=0\\\\a=24\texttt{ or }a=-25`

Since a is negative we can avoid answer 24.

So value of a is -25.

Other integer is a+1 = -24.

Lesser integer = -25