Question

A Ladder that is 32 ft long leans against a building. The angle of elevation of the ladder is 70. To the nearest tenth of a foot how high off the ground is the top of the ladder?

A. 20.3 ft

B. 10.9 ft

C. 26.2 ft

D. 39.1 ft

Answer 1

This is a classic right triangle trig problem. The ladder leaning against the building serves as the hypotenuse of the triangle, the angle of elevation is the angle created by the ground and the ladder, and where the ladder meets the building is the leg opposite the angle (or the height of the triangle). Use the sin ratio to find the height of the ladder up the building. Sin(70) = x/32. Multiply both sides by 32 to get 32sin70=x and x = 30.07. (You mistyped the D answer, I'm assuming. Do this on your calculator to see)

Answer 2

The correct option is B.

Explanation:

It is given that a Ladder that is 32 ft long leans against a building. The angle of elevation of the ladder is 70.

Let the distance between ground and the top of the ladder be x.

In a right angled triangle,

`\cos\theta=(base)/(perpendicular)`

`\cos(70^(\circ))=(x)/(32)`

`30\cos(70^(\circ))=x`

`10.9446=x`

`x\approx 10.9`

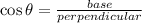
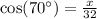
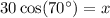
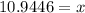
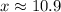
The distance between ground and the top of the ladder is 10.9 ft. Therefore the correct option is B.