Question

the pentagonal prism has a perpendicular distance of 14 units between the bases. The volume of the prism is 840 cubic units. What is the perimeter of the base?

Answer 1

30 rounded

Explanation:

Answer 2

The volume of a prsm is given by the area of the base multiplied by the height.

Given a pentagonal prism with a perpendicular distance of 14 units between the bases and a volume of 840 cubic units. This means that the height of the prism is 14 units.

i.e. Area of base x 14 = 840
which implies that the area of the base = 840 / 14 = 60

Assuming that the pentagonal base is regular.
Area of the pentagon base is given by

`A= (1)/(4) \sqrt{5(5+2 √(5)) } a^2`
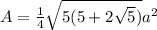
where a is the length of the sides.

`60= (1)/(4) \sqrt{5(5+2 √(5)) } a^2 \\ \\ \sqrt{5(5+2 √(5)) } a^2=240 \\ \\ a^2= \frac{240}{\sqrt{5(5+2 √(5)) }} =34.8740 \\ \\ a=5.9054`

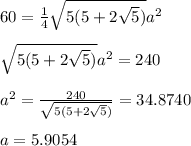
Perimeter of a pentagon is given by 5a
where a is the length of the sides.

Therefore,. the perimeter of the base of the pentagonal prism is given by 5 x 5.9054 = 29.5 units.