Question

the equation a= 180(n-2)/n represents the angle measures, a, in a regular n-sided polygon. When the equation is solved for n, n is equal to a fraction with a denominator of a – 180. What is the numerator of the fraction?

Answer 1

`a= (180(n-2))/(n) \\ an=180n-360 \\ an-180n=-360 \\ n(a-180)=-360 \\ n= (-360)/(a-180)`

numerator of the fraction is -360.

Answer 2

-360.

Explanation:

We have been give an equation
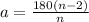`a=( 180(n-2))/(n)`, which represents the angle measures, a, in a regular n-sided polygon. We are asked to find the numerator of the fraction, while solving our equation for n.

Let us multiply both sides of our equation by n.

`a*n=n*( 180(n-2))/(n)`

`a*n= 180(n-2)`

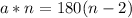
Upon distributing 180 we will get,

`a*n= 180n-360`

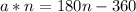
Let us subtract 180n to both sides of our equation.

`a*n-180n= 180n-180n-360`

`a*n-180n=-360`

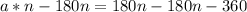
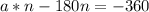
Let us factor out n from left hand side of our equation.

`n(a-180)=-360`

Let us divide both sides of our equation by a-180.

`(n(a-180))/((a-180))=(-360)/((a-180))`

`n=(-360)/((a-180))`

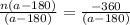
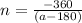
Therefore, the numerator of our fraction with a denominator of (a-180) will be -360.