Question

In the diagram, mFLI is 106°, mFLG = (2x – 1)°, mGLH = (x + 17)°, and mHLI = (4x – 15)°.

What is the measure of the smallest angle in the diagram?

15°29°32° 45°

Answer 1

29*

Explanation:

Answer 2

Step
`1`

Find the value of x

we know that

m∠FLI=m∠FLG+m∠GLH+m∠HLI ---------> equation
`1`

In this problem we have

m∠FLI=
`106`°

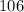m∠FLG=
`(2x-1)`°

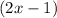m∠GLH=
`(x+17)`°

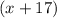m∠HLI=
`(4x-15)`°

Substitute the values in the equation
`1`

`106=(2x-1)+(x+17)+(4x-15)`

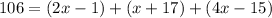
Combine like terms

`106=(2x+x+4x)+(-1+17-15)`

`106=(7x)+(1)`

`7x=105`

`x=15`°

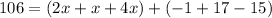
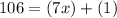
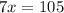
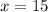Step
`2`

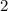
Find the value of each angle

Substitute the value of x in each angle

m∠FLG=
`(2*15-1)=29`°

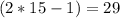m∠GLH=
`(15+17)=32`°

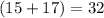m∠HLI=
`(4*15-15)=45`°

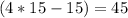therefore

the answer is

The smallest angle in the diagram is
`29\ degrees`