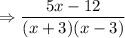Question

What is the sum?

3/x^2-9 + 5/x+3
A) 8/x^2+x-6
B) 5x-12/x-3
C)-5x/(x+3(x-3)
D) 5x-12/x+3(x-3)

Answer 1

Sum
`\Rightarrow (5x-12)/((x+3)(x-3))`

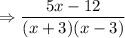
D is correct

Explanation:

Given:
`(3)/(x^2-9)+(5)/(x+3)`

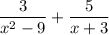
We are given a rational expression and to add the expression.

First we make common denominator and then we add them

Multiply and divide the second fraction by x-3

`\Rightarrow (3)/(x^2-9)+(5(x-3))/((x-3)(x+3))`

`\Rightarrow (3)/(x^2-9)+(5x-15)/(x^2-9)`

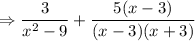
Now we have common denominator and write as common

`\Rightarrow (3+5x-15)/(x^2-9)`

`\Rightarrow (5x-12)/(x^2-9)`

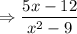
Factor the denominator:
`a^2-b^2=(a-b)(a+b)`

`\Rightarrow (5x-12)/((x+3)(x-3))`

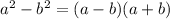
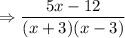
Hence, The sum is
`\Rightarrow (5x-12)/((x+3)(x-3))`

Answer 2

We will use the formula a^2-b^2=(a-b)(a+b) to get the fractions to the same dominator.

3/[(x-3)(x+3)]+5/(x+3) =
3/[(x-3)(x+3)]+5(x-3)/(x+3)[(x-3)(x+3)] =
(3+5x-15)/[(x-3)(x+3)] =
(5x-12)/[(x-3)(x+3)]

The final answer is D.