Question

How many stones will it take to build the wall shown if each stoke measured 6 1/2 in x 15 1/2 in. Including mortar. Please help me on this. I'm so confused.

Answer 1

240 stokes

Step-by-step explanation

Step 1

find the area of the wall

remember the area of a rectangle is given by:

`\text{Area}_(rec)=\text{ length}\cdot width`

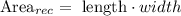
then

let.

`\begin{gathered} length=31^(\prime)\text{ } \\ \text{ width= }=5^(\prime)5^(\doubleprime) \end{gathered}`

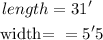
to operate , we need to have the same unit of measure, so we need to convert ft(') into inch(')

remember that

12 inches = 1 ft

hence

`\begin{gathered} length=31^(\prime)\text{ }=31\text{ ft=31 ft(}\frac{12\text{ in}}{1\text{ ft}}\text{)=3}72\text{ inches} \\ \text{ width= }=5^(\prime)5^(\doubleprime)=5\text{ ft+5 in=5 ft(}\frac{12\text{ in}}{1\text{ ft}}\text{)}+\text{ 5 in=60 in+5 in=65 inches} \end{gathered}`

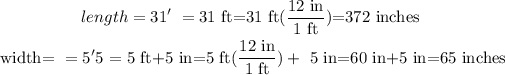
now, replace in the formula to find teh area of the wall

`\begin{gathered} \text{Area}_(rec)=\text{ length}\cdot width \\ A=372\text{ in}\cdot\text{ 65 in} \\ A=24180(in)^2 \end{gathered}`

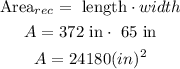
Area of the wall = 24180 squared inches

Step 2

now, we to find the area of each stoke ( also a rectangle)

then

Let

`\begin{gathered} \text{length = 15 }(1)/(2)in \\ \text{width}=\text{ 6 }(1)/(2)\text{ in} \end{gathered}`

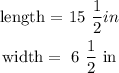
to operate we need to convert the mixed numbers into improper fractions,

remember how to do that

`a(b)/(c)=((a\cdot c)+b)/(c)`

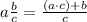
therefore,

`\begin{gathered} 15\text{ }(1)/(2)=((15\cdot2)+1)/(2)=(31)/(2) \\ \text{and} \\ 6(1)/(2)=((6\cdot2)+1)/(2)=(13)/(2) \end{gathered}`

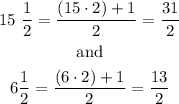
so

`\begin{gathered} \text{length = }(31)/(2)in \\ \text{width}=\text{ }(13)/(2)\text{ in} \end{gathered}`

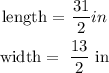
now, let's replace in the formula to find the area of each stoke

`\begin{gathered} \text{Area}_(rec)=\text{ length}\cdot width \\ A=(31)/(2)in\cdot(13)/(2)in \\ A=(403)/(4)=100.75\text{ squared inches} \\ A=100.75(in)^2 \end{gathered}`

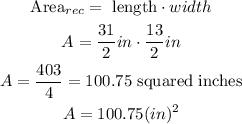
Area of echa stoke: 100.75 squared inches

Step 3

Finally, to get the number of stones that will take to build the wall, we need to divide the total area, by the area of one stoke

so

`\text{ number of stokes required=}\frac{area\text{ of the wall}}{\text{area of each stoke}}`

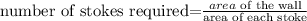
replace

`\text{number of stokes required=}(24180(in)^2)/(100.75((in)^2)=240`

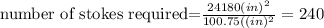
hence

the answer is

240 stokes

I hope this helps you