Question

A rectangle with constant area has possible lengths and widths as shown in the table below. Width vs. Length of a Rectangle Width (w) Length (l) 2 37.5 4 18.75 6 12.5 8 9.375 Which equation can be used to find any corresponding length and width that fits the pattern in this table?

Answer 1

The answer is. A) I= k/w Where I is the length, w is the width, and k is a constant

Answer 2

Given: A rectangle with constant area has possible lengths and width as shown in the given table.

Inverse variation states that a relationship between two variables in which the product is a constant.

If one variable increases, the other decreases in proportion so that the product is unchanged.

i.e, if b is inversely proportional to a i.e,
`y \propto (1)/(x)` , the equation is of the form

`b= (k)/(a)` or ab = k , where k is constant of variation.

As, you can see from the table as width(w) increases, the length decreases so ,it is an inverse variation.

By area of rectangle formula:
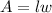`A =lw` where l is the length and w is the width respectively;

Since, Area is constant i.e,

`A = 2 * 37.5 = 75`

`A = 4 * 18.75 = 75` ....

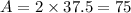
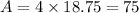Therefore, the equation which is used to find any corresponding length and width that fits the pattern in this table is:
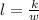`l = (k)/(w)` or lw = k ; where k is the constant area.