Question

Which statements describe the graph of y = 3√x-1+2 ? Check all that apply.

The graph has a domain of all real numbers.
The graph has a range of y 1.
As x is increasing, y is decreasing.
The graph has a y-intercept at (0, 1).
The graph has an x-intercept at (–7, 0).

Answer 1

Answer: option A, D and E

Explanation:

Answer 2

The correct options are A, D and E.

Explanation:

We are given the function
`y=\sqrt[3]{x-1} +2`

From the graph below, we see that,

Domain and range of the function is the set of all real numbers.

As y-intercept is the point where the graph of the function crosses y-axis.

That is, y-intercept is obtained when x= 0.

So, on substituting, we have,

`y=\sqrt[3]{0-1} +2`

i.e.
`y=-1+2`

i.e. y= 1

Thus, the y-intercept is (0,1).

Also, x-intercept is the point where the graph of the function crosses x-axis.

That is, x-intercept is obtained when y= 0.

So, on substituting, we have,

`0=\sqrt[3]{x-1} +2`

i.e.
`-2=\sqrt[3]{x-1}`

i.e.
`-8=x-1`

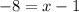
i.e. x= -7

Thus, the x-intercept is (-7,0).

Hence, the correct options for the function are,

A. The graph has a domain of all real numbers.

D. The graph has a y-intercept at (0, 1)

E. The graph has an x-intercept at (–7, 0).