Question

The vertices of a quadrilateral ABCD are A(4, 8), B(10, 10), C(10, 4), and D(4, 4). The vertices of another quadrilateral EFCD are E(4, 0), F(10, −2), C(10, 4), and D(4, 4). Which conclusion is true about the quadrilaterals?

A) The measure of their corresponding angles is equal.
B) The ratio of their corresponding angles is 1:2.
C) The ratio of their corresponding sides is 1:2
D) The size of the quadrilaterals is different but shape is same.

Answer 1

The size of the quadrilaterals is different but shape is same.

Answer 2

The correct option is A.

Explanation:

It is given that the vertices of a quadrilateral ABCD are A(4, 8), B(10, 10), C(10, 4), and D(4, 4).

The vertices of another quadrilateral EFCD are E(4, 0), F(10, −2), C(10, 4), and D(4, 4).

The relation between vertices of ABCD and EFCD is defined as

`(x,y)\rightarrow (x,8-y)`

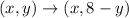
It means the figure ABCD reflected across the line y=4 to get the quadrilateral EFCD.

From the below figure it is clear that the quadrilateral ABCD reflected across the line y=4 to get the quadrilateral EFCD.

Reflection is a rigid transformation, it means the size and shape of the quadrilaterals is same. In other words quadrilateral ABCD and quadrilateral EFCD are congruent.

The corresponding parts of congruent triangles are congruent. So, the measure of their corresponding angles is equal.

Therefore the correct option is A.