Question

A screwdriver

is dropped from the top of an elevator shaft
.
Exactly 6.0

seconds​ later, the sound of the screwdriver

hitting bottom is heard. How deep is the shaft
​?
​(Hint: The distance that a dropped object falls in t seconds is represented by the formula sequals
16tsquared
.
The speed of sound is 1100​ ft/sec.)

Answer 1

jpniwed ccjip eafvwrojfnqejnvejnfejrnfejr vv erjv erijv eirjerjv ev ejvre j

Answer 2

495.92 m

Explanation:

Let h be the height of the shaft

t = Time taken by the screwdriver to fall to the ground

Time taken to hear the sound is 6 seconds

Time taken by the sound to travel the height of the shaft = 6-t

Speed of sound in air = 1100 ft/s

For the stone falling

`s=ut+(1)/(2)at^2\\\Rightarrow h=0t+(1)/(2)* 32.2* t^2\\\Rightarrow h=(1)/(2)* 32.2* t^2`

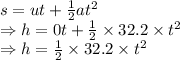
For the sound

Distance = Speed × Time

`\text{Distance}=1100* (6-t)`

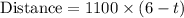
Here, distance traveled by the screwdriver and sound is equal

`(1)/(2)* 32.2* t^2=1100* (6-t)\\\Rightarrow 16.1t^2+1100t-6600=0\\\Rightarrow 161t^2+11000t-66000=0`

`t=(-11000+√(11000^2-4\cdot \:161\left(-66000\right)))/(2\cdot \:161), t=(-11000-√(11000^2-4\cdot \:161\left(-66000\right)))/(2\cdot \:161)\\\Rightarrow t=5.55, -73.87`

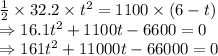
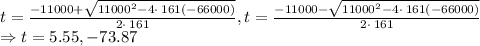
The time taken to fall down is 5.55 seconds

`h=(1)/(2)* 32.2* 5.55^2=495.92\ m`

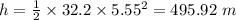
Height of the shaft is 495.92 m