Question

A science test, which is worth 100 points, consists of 24 questions. Each question is worth either 3 points or 5 points. If x is the number of 3-point questions and y is the number of 5-point questions, the system shown represents this situation. x + y = 24 3x + 5y = 100 What does the solution of this system indicate about the questions on the test? The test contains 4 three-point questions and 20 five-point questions. The test contains 10 three-point questions and 14 five-point questions. The test contains 14 three-point questions and 10 five-point questions. The test contains 20 three-point questions and 8 five-point questions.

Answer 1

x+y=24 so we can say

x=24-y making 3x+5y=100 become

3(24-y)+5y=100

72-3y+5y=100

72+2y=100

2y=28

y=14, since x=24-y

x=10

So there are 10 3-point questions and 14 5-point questions.

Answer 2

The test contains 10 three-point questions and 14 five-point questions.

Explanation:

We are given that A science test, which is worth 100 points, consists of 24 questions. Each question is worth either 3 points or 5 points

System of equations:
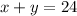`x+y=24` --a

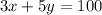`3x+5y=100` --b

Where x denotes x is the number of 3-point questions and y is the number of 5-point questions

Now solve equation a and b by substitution method

Substitute the value of x from a in b

⇒
`3(24-y)+5y=100`

⇒
`72-3y+5y=100`

⇒
`72+2y=100`

⇒
`2y=28`

⇒
`y=(28)/(2)`

⇒
`y=14`

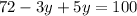
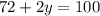
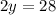
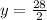
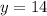
Substitute the value of y in equation a to get the value of x

`x+14=24`

`x=10`

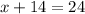
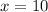
Thus 10 is the number of 3-point questions.

14 is the number of 5-point questions.

Thus Option 2 is correct.

The test contains 10 three-point questions and 14 five-point questions.