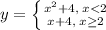Question

Which of the following functions is graphed below? Please help!!

Answer 1

The answer is choice C.

The hole is attached to the graph for x^2+4 which means that we do NOT include this as part of the graph. The graph x^2+4 is only graphed when x < 2 is true which is what choice C says. Similarly, x+4 is only graphed when x >= 2.

Answer 2

The correct option is C.
`y=\left \{ {x^2+4, \; x<2} \atop {x+4, \;x\geq 2}} \right.`

Explanation:

Consider the provided graph:

The graph has an open and closed dot at x = 2.

The open dot attached to the function
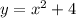`y=x^(2)+4` and the closed dot attached to the function
`y=x+4`.

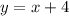Note, we use
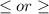`\leq or \geq` sign in order to show closed dots and < or > sign to show open dots.

By observing the graph, it is clear that the function
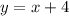`y=x+4` takes all the value which are greater or equal to 2. Therefore, the function can be written as
`y=x+4, x\geq 2`.

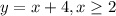The graph of the function
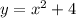`y=x^(2)+4` has an open dot at
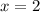`x = 2` which means the function can take all real values less than 2. Therefore, the function can be written as
`x^2+4, x<2`.

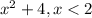Therefore, the correct option is C.
`y=\left \{ {x^2+4, \; x<2} \atop {x+4, \;x\geq 2}} \right.`