Question

What is the most precise name for quadrilateral ABCD with vertices A(-3,2), B(-1,4), C(4,4) and D(2,2).

Answer 1

Answer with explanation:

The Vertices of Quadrilateral A B CD are , A(-3,2), B(-1,4), C(4,4) and D(2,2).

To determine the unique Quadrilateral,we will

1. Find the side lengths.

2. Length of Diagonals

3. Check whether diagonals bisect each other or not.

4.Slope between two sides

Side length

Formula to find Distance between two points (p,q) and (a,b)

`\sqrt{(p-a)^2+(q-b)^2`

`AB=√((-3+1)^2+(2-4)^2)}=√(8)=2√(2)\\\\ BC=√((4+1)^2+(4-4)^2)=5\\\\CD=√((2-4)^2+(2-4)^2)=√(4+4)=2√(2)\\\\DA=√((2+3)^2+(2-2)^2)=5`

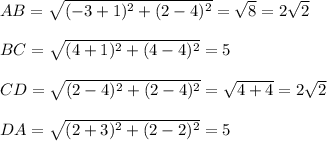
→AB=CD , And ,BC=DA------Opposite sides are equal.

Length of Diagonal

`AC=√((4+3)^2+(4-2)^2)=√(7^2+2^2)\\\\AC=√(53)\\\\BD=√((2+1)^2+(2-4)^2)\\\\BD=√(9+4)=√(13)`

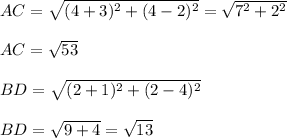
AC≠BD

Mid point of Diagonals

→Mid point can be calculated by section formula,known as mid point formula

Mid point of AC

`((4-3)/(2),(4+2)/(2))=((1)/(2),3)`

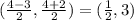
Mid point of BD

`((2-1)/(2),(2+4)/(2))=((1)/(2),3)`

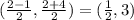
Diagonals Bisect each other.

It can't be a rectangle , because length of diagonals are not equal.

The given quadrilateral is a parallelogram,because

1. Opposite sides are equal.

2. Diagonals bisect each other.

→→→→Most precise Name of quadrilateral ABCD with vertices A(-3,2), B(-1,4), C(4,4) and D(2,2)= Parallelogram