Question

In the figure, the perimeter of hexagon ABCDEF is approximately 93 units, and its area is ____square units.

Answer 1

The hexagon is composed of two trapezoids (both of which are congruent). Let's find the area of the top trapezoid

A = h*(b1+b2)/2
A = 10*(40+10)/2
A = 10*(50)/2
A = 500/2
A = 250

Each trapezoid has area of 250 square units. So the combined area is 2*250 = 500 square units

The area of the hexagon is 500 square units.

Answer 2

`500\text{ units}^2`

Explanation:

We have been been given an image of hexagon ABCDEF and we are asked to find the area of our given hexagon.

Upon looking at our given diagram, we can see that it consists two congruent trapezoids, so the area of our given hexagon will be 2 times the area of trapezoid ABCF.

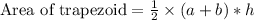`\text{Area of trapezoid}=(1)/(2)* (a+b)*h`, where, a and b are bases of trapezoid and h is height of trapezoid.

`\text{Area of trapezoid}=(1)/(2)* (AB+CF)*h`

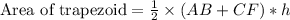
We can see that height of our given trapezoid is 10 as the altitude from point A will be 10 units on x-axis.

`\text{Area of trapezoid}=(1)/(2)* (10+40)*10`

`\text{Area of trapezoid}=(50)*5`

`\text{Area of trapezoid}=250`

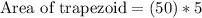
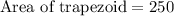
Since the area of two times the area of hexagon ABCF, so we wil multiply 250 by 2 to get the area of trapezoid.

`\text{Area of hexagon}=2* 250`

`\text{Area of hexagon}=500`

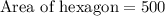
Therefore, the area of our given hexagon is 500 square units.