Question

the ratio of surface areas of two similar solids is equal to the square root of the ratio between their corresponding edge lengths. true or false

Answer 1

False.

Explanation:

Let us consider two similar cuboids A and B as shown in the figure below.

We have that,

'A' has length, width and height 5, 3 and 4 units respectively.

'B' has length, width and height 7.5, 4.5 and 6 units respectively.

Also, surface area of a cuboid = 2 × ( L + W + H ), where L= length, W= width and H= height.

Now, we will find the surface area of A and B.

Surface area of A,
`S_(A)` = 2 × ( 5 + 3 + 4 ) = 2 × 12 = 24

Surface area of B,
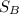`S_(B)` = 2 × ( 7.5 + 4.5 + 6 ) = 2 × 18 = 36

Therefore, the ratio of the surface area is
`S_(A)` :
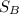`S_(B)` = 24 : 36 = 2 : 3.

Moreover, the ratio of square root of lengths is given by
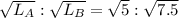`\sqrt{L_(A)} : \sqrt{L_(B)} = √(5) : √(7.5)` = 2.24 : 2.74

Hence, we see that the ratio of the surface area of two similar solids is not equal to the square root of the ratio between their corresponding edge lengths.