the length of the trainning track is 361.26 m
Step-by-step explanationto find the length of the training track we need to add twice the length of the rectangle ot the circumference of the circle ,so
Step 1
so
Perimeter=2(Length)+2 ( area of half circle/2)
Perimeter=2(L1)+ area of a circle
hence
a)let
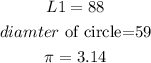
so
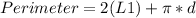
replace and calculate
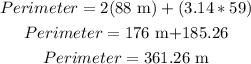
therefore, the length of the trainning track is 361.26 m
I hope this helps you