Question

A training field is formed by joining a rectangle and two semicircles, as shown below. The rectangle is long and wide. What is the length of a training track running around the field? (Use the value for , and do not round your answer. Be sure to include the correct unit in your answer.)

Answer 1

the length of the trainning track is 361.26 m

Step-by-step explanation

to find the length of the training track we need to add twice the length of the rectangle ot the circumference of the circle ,so

Step 1

so

Perimeter=2(Length)+2 ( area of half circle/2)

Perimeter=2(L1)+ area of a circle

hence

a)let

`\begin{gathered} L1=88 \\ diamter\text{ of circle=59} \\ \pi=3.14 \end{gathered}`

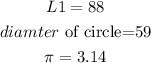
so

`Perimeter=2(L1)+\pi *d`

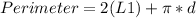
replace and calculate

`\begin{gathered} Perimeter=2(88\text{ m})+(3.14*59) \\ Perimeter=176\text{ m+185.26} \\ Perimeter=361.26\text{ m} \end{gathered}`

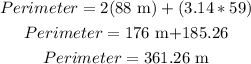
therefore, the length of the trainning track is 361.26 m

I hope this helps you