1 Answer

Pedro S Cord · Answer 1 · 2023-04-20T08:51:10+0000

The data set is:

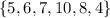
$\mleft\lbrace5,6,7,10,8,4\mright\rbrace$

a) The variance of a data set is given by the formula:

$s^2=(1)/(N-1)\sum ^N_(n\mathop=1)(a_n-\operatorname{mean})^2$

Where s^2 is the variance and P(a_n) is the probability of the value a_n.

First, we need to calculate the mean of the data set:

$\operatorname{mean}=((5+6+9+10+8+4))/(6)=(42)/(6)=7$

Now, the variance is:

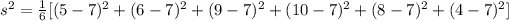
$s^2=(1)/(6)\lbrack(5-7)^2+(6-7)^2+(9-7)^2+(10-7)^2+(8-7)^2+(4-7)^2\rbrack$

Then,

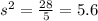
Therefore, the variance is equal to 5.6

b) As for the standard deviation, we simply need to get the square root of the variance. Then,

$\text{Standard deviation}=\sqrt[]{s^2}=\sqrt[]{5.6}\approx2.3664$

The standard deviation is 2.3664 approximately

Your comment on this question: