We are given the mean and standard deviation for the profitability of companies that changed their names.
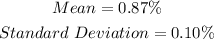
Chebyshev's Theorem states that the estimated percentage of data falling within k standard deviations is equal to
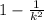
To find the percentage of companies with relative stock price increases between 0.67% and 1.07%, we must first solve for k.
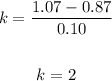
Then we use k =2 in Chebyshev's formula.
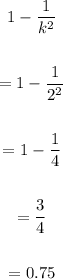
The answer is 0.75 or 75%.
For part b, we will use the following equation:
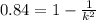
Solving for k, we get:
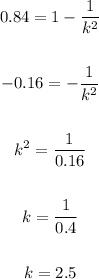
This means that the boundaries are 2.5 standard deviations away from the mean.
![\begin{gathered} Lower\text{ }boundary=0.87\%-(2.5*0.10\%) \\ Lower\text{b}oundary=0.87\operatorname{\%}-0.25\% \\ Lower\text{b}oundary=0.62\% \end{gathered}]()
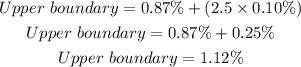
The answers are 0.62% and 1.12%.