So we have 7 different graphs. Their respective functions have the following form:
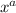
We need to find the value of a on each case. One thing to notice before starting is that some of the possible values for a are negative. A negative exponent means:
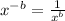
This means that any function with a negative a presents an asymptote in x=0. This means that their graphs increase or decrease sharply along the y axis. Another important thing to note is that if a is a rational number and its divider is even then the graph of the function is only defined for postive x values.
So let's start with graph a. As you can see there's no asymptote and the graph is defined for negative x values. These two characteristics tell us that the exponent a can be 8/5 or 5/3. Now let's choose a random x value. Let's say x=-1 and see the result for both cases:
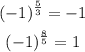
If we look at the graph we can see that for negative x values the function must be negative. This is the cas of 5/3 and not of 8/5. Then in a) a=5/3.
And that's the first answer, now let's see the second. Here there's no asymptote (so a is greater than 0) and the function is defined for negative x values (so the dividerof a is odd) which leave these possible values for a: 1/5, 8/5 and 6/11 (we can discard 5/3 since it was already used). As we already saw if a=8/5 then the graph in x=-1 must be positive. However, graph b is negative for negative x values so 8/5 can also be discarded. So we only have 1/5 and 6/11. Let's see what happens to x=-1 in both cases:
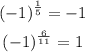
Since the result must be a negative number then the answer for b) is a=1/5.
Now in graph c there is no asymptote and the graph its defined for negative values so again, a is not negative nor it has an even divider. This give us three options: 1/5, 5/3 and 8/5. Since the first two were already used we can conclude that in c) a=8/5.
Now let's see graph d. It has an asymptote in x=0 and it's defined for negative x so a is negative and its divisor is odd. Then we have two options: -1/3 and -4/3. Again let's see the values of both possible functions for x=-1:
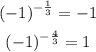
Looking at the graph the value for x=-1 must be negative so the answer for d) is a=-1/3.
Now let's see graph e. There's no asymptote and there's no graph for negative x values. This means that a is positive and has an even divider so we have these options: 3/4 and 5/8. Looking at the graph you can see that at x=3 the graph is in y=2. Let's see the y values of both possibilities when x=3:
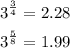
The one with a=5/8 is closer to y=2 so the answer for e) is a=5/8.
Now we take a look to graph f. It has an asymptote in x=0 and its only defined for positive x values so a is negative and has an even divider. There's only one option that meets these two requirements and that is -1/4 so the answer for f) is a=-1/4.
Finally we have graph g. It's defined for both positive and negative x values and it has no asymptote so a is positive and has an odd divider. Then we have several options for a: 1/5, 8/5, 5/3 and 6/11. The first three are already used so the only option is 6/11. Then in g) a=6/11.