Question

Frank kicks a soccer ball off the ground and in the air, with an initial velocity of 30 feet per second. Using the formula H(t) = −16t2 + vt + s, what is the maximum height the soccer ball reaches?

Answer 1

The answer is A or 14.1

Answer 2

A quadratic equation is in the form of
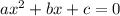`ax^2+bx+c =0` then the axis of symmetry is given by:

`x = (-b)/(2a)`

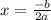
Given the equation:

`H(t) = -16t^2+vt+s`

where,

v is the initial velocity

s is the initial height.

Frank kicks a soccer ball off the ground and in the air, with an initial velocity of 30 feet per second.

⇒
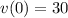`v(0) = 30`feet per second.

Substitute in [1] we have;

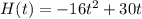`H(t) = -16t^2+30t` ....[1]

then:

the axis of symmetry is:

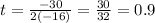`t = (-30)/(2(-16)) = (30)/(32) = 0.9` sec

Substitute in [1] we have;

`H(0.9) = -16(0.9)^2+30(0.9)`

⇒
`H(0.9) = -12.96+27`

⇒
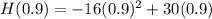
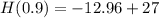
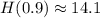`H(0.9) \approx 14.1` feet

Therefore,the maximum height the soccer ball reaches is, 14.1 feet