Question

A triangle with vertices at A(20, –30), B(10, –15), and C(5, –20) has been dilated with a center of dilation at the origin. The image of B, point mc017-1.jpg, has the coordinates (2, –3). What is the scale factor of the dilation?

Answer 1

I think it's B hope this helps out

Answer 2

The scale factor of the dilation is
`(1)/(5)`.

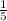Explanation:

Given information: A triangle with vertices at A(20, –30), B(10, –15), and C(5, –20). The center of dilation at the origin. The image of B has the coordinates (2, –3).

If a figure dilated with a center of dilation at the origin and scale factor k, then

`P(x,y)\rightarrow P'(kx,ky)`

`B(10,-15)\rightarrow B'(k(10),k(-15))`

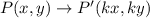
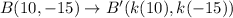
Since the image of B has the coordinates (2, –3), therefore

`B'(10k,-15k)=B'(2,-3)`

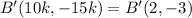
On comparing both sides, we get

`10k=2`

`k=(2)/(10)=(1)/(5)`

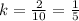
Therefore the scale factor of the dilation is
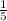`(1)/(5)`.