Question

What is the value of x?

x=
units

Answer 1

Answer: The value of x is 12 units.

Step-by-step explanation: We are given to find the value of x from the figure.

We can see that triangle RSQ is a right-angled one with m∠SRQ = 90°. And RT is perpendicular to the hypotenuse SQ.

Given ST = 9 units, TQ = 16 units and RT = x = ?

Since ΔRSQ is a right-angled triangle with hypotenuse SQ and RT is perpendicular to SQ, so we must have

`RT^2=ST* TQ\\\\\Rightarrow x^2=9* 16\\\\\Rightarrow x^2=144\\\\\Rightarrow x=\pm √(144)\\\\\Rightarrow x=\pm12.`

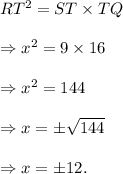
Since the length of a line segment cannot be negative, so the value of of x is 12 units.

Thus, the required value of x is 12 units.

Answer 2

By Pythagoras theorem


`RQ^(2)= x^(2) + 16^(2)`

`RS^(2)= x^(2) + 9^(2)`


`SQ^(2)= RS^(2) + RQ^(2)`

`SQ^(2)= x^(2) + 16^(2) + x^(2) + 9^(2)`

`SQ^(2)=2 x^(2) +256+81`

`25^(2)=2 x^(2) +337`

`625-337=2 x^(2)`

`288=2 x^(2)`

`144= x^(2)`

`x=12`