Question

A student scored 84 and 87 on her first two quizzes.Write and solve a compound inequality to find the possible values for a third quiz score that would give her an average between 85 and 90 inclusive.

Answer 1

The score in third quiz must be lie between 84 to 99 inclusive.

Explanation:

Let the marks in third quiz be x.

The student scored 84 and 87 on her first two quizzes.

The formula for mean is

`Mean=\frac{\text{Sum of observations}}{\text{No. of observations}}`

`Mean=(84+87+x)/(3)`

`Mean=(171+x)/(3)`

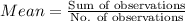
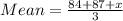
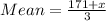
The average between 85 and 90 inclusive.

`85\leq(171+x)/(3)\leq90`

`85* 3\leq171+x\leq 90* 3`

`255\leq171+x\leq 270`

`255-171\leq x\leq 270-171`

`84\leq x\leq 99`

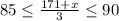
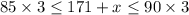
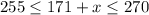
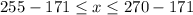
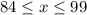
Since the value of x lies between between 84 to 99 inclusive, therefore the score in third quiz must be lie between 84 to 99 inclusive.

Answer 2

Mean of data = sum of values ÷ number of data

We have three values; 84, 87, and
`x`

Sum of values =
`84+87+x` =
`171+x`

We want the value of
`x` to give mean between 85 and 90 inclusive


`85 \leq (171+x)/(3) \leq 90`

`85*3 \leq 171+x \leq 90*3`

`255 \leq 171+x \leq 270`

`255-171 \leq x \leq 270-171`

`84 \leq x \leq 99`

Hence, the value of
`x` is between 84 and 99 inclusive