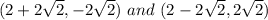Question

X+y=2 y=-1/4x^2+3 In two or more complete sentences, explain how to solve the system of equations algebraically. Solve the system of equations. In your final answer, include all of your work.

THIS IS AN ESSAY!!!

Answer 1

Answer with explanation:

We are given a system of equation as:

`x+y=2-----------(1)\ ;\ y=(-1)/(4)x^2+3------------(2)`

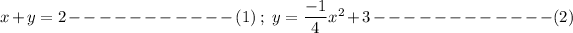
• We solve the system by the method of substitution.

i.e. we substitute the value of y from equation (2) into equation (1) and find the value of x.

and finally putting the value of x back to equation (2) and get the value of y.

• Hence, we solve the equation as follows:

We put the value of y from equation (2) into equation (1) to get:

`x-(1)/(4)x^2+3=2\\\\\\i.e.\\\\x-(1)/(4)x^2=2-3\\\\i.e.\\\\x-(1)/(4)x^2=-1\\\\\\i.e.\\\\4x-x^2=-4\\\\i.e.\\\\x^2-4x-4=0`

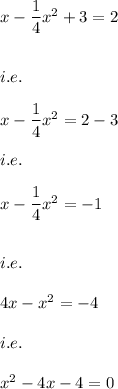
The solution of the quadratic equation:

`ax^2+bx+c=0`

is given by:

`x=(-b\pm √(b^2-4ac))/(2a)`

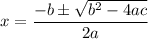
Here,

`a=1,\ b=-4\ and\ c=-4`

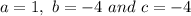
Hence, the solution is:

`x=(4\pm √((-4)^2-4* (-4)* 1))/(2* 1)\\\\i.e.\\\\\\x=(4\pm √(32))/(2)\\\\i.e.\\\\x=(4\pm 4√(2))/(2)\\\\i.e.\\\\x=2\pm 2√(2)`

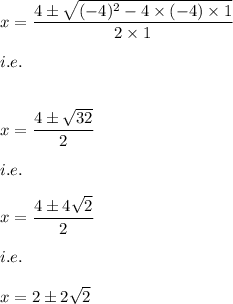
Case--1:

Now,

when
`x=2+2√(2)`

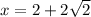
Then

`y=(-1)/(4)(2+2√(2))^2+3\\\\i.e.\\\\y=(-1)/(4)[4+8+8√(2)]+3\\\\i.e.\\\\y=(-1)/(4)[12+8√(2)]+3\\\\i.e.\\\\y=-3-2√(2)+3\\\\i.e.\\\\y=-2√(2)`

Case--2:

Now,

when
`x=2-2√(2)`

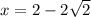
`y=(-1)/(4)(2-2√(2))^2+3\\\\i.e.\\\\y=(-1)/(4)[4+8-8√(2)]+3\\\\i.e.\\\\y=(-1)/(4)[12-8√(2)]+3\\\\i.e.\\\\y=-3+2√(2)+3\\\\i.e.\\\\y=2√(2)`

Hence, the solution to the system are:

`(2+2√(2),-2√(2))\ and\ (2-2√(2),2√(2))`

Answer 2

hello :
x+y = 2.....(1)
y= (-1/4)x²+3...(2)
by (1) : y = -x+2
subsct in (2) : -x +2 =( -1/4)x²+3
-4x+8 = -x² +12
x²-4x - 4 =0
(x² -4x +4) -4 -4 =0
(x-2)² = 8 =(2√2)²
x-2 = 2√2 or x-2 = - 2√2
x= 2+ 2√2 or x= 2- 2√2
if : x= 2+ 2√2 .....y = -( 2+ 2√2 )+2 = - 2√2
if : x= 2- 2√2 .....y = -( 2- 2√2 )+2 = 2√2
two solutione : (2+ 2√2 , - 2√2 ) , (2- 2√2 , 2√2 )