Question

A 0.015-kg ball is shot from the plunger of a pinball machine. because of a centripetal force of 0.028 n, the ball fol- lows a circular arc whose radius is 0.25 m. what is the speed of the ball?

Answer 1

Centripetal force is F=mv^2/r.
So v=Sqrt (Fr/m)=(.028•0.25/0.015)^(1/2)=0.683m/s

Answer 2

Answer: The speed of the ball is 0.68 m/s

Step-by-step explanation:

To calculate the speed of the ball, we use the equation used to calculate centripetal force:

`F=(mv^2)/(r)`

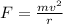
where,

F = centripetal force = 0.028 N

v = speed of the ball = ?

m = mass of the ball = 0.015 kg

r = radius of the ball = 0.25 m

Putting values in above equation, we get:

`0.028=(0.015* (v)^2)/(0.25)\\\\v=\sqrt{(0.25* 0.028)/(0.015)}=0.68m/s`

Hence, the speed of the ball is 0.68 m/s