Question

A roller coaster has a mass of 500 kg. It drops from rest at the top of a hill that's 57 m tall. How fast is it going when it reaches the bottom? Acceleration due to gravity is g = 9.8 m/s2.

Answer 1

The answer should be 33.4m/s

Answer 2

`v=33.42 (m)/(5)`

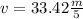
Step-by-step explanation:

Hello

The principle of conservation of energy indicates that energy is not created or destroyed; It only is transformed in some ways into others. In these transformations, the total energy remains constant; that is, the total energy is the same before and after each transformation.in this case the potential energy is the mechanical energy associated with the location(heigth) Ec=mgh, here m is the mass, g is the acceleration due to gravity and h is the height

`E_(g)=mgh`

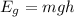
and , it must be equal to the kinetic energy in the bottom, it is given by

`E_(k)=(mv^(2))/(2)\\`

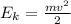
where m is the mass of the object , and v its velocity

According to the principle of conservation of energy

`E_(g)=E_(k)\\mgh=(mv^(2) )/(2) \\Now, isolate\ v\\gh=(v^(2) )/(2) \\2gh=v^(2)\\√(2gh) =v\\`

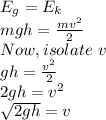
the velocity only can be positive, it means we need just the positive root

Replacing

`v= √(2gh) \\v= \sqrt{2(9.8 (m)/(s^(2) ) )*57m} \\v=\sqrt{(117.2m^(2) )/(s^(2) ) } \\v=33.42 (m)/(5)`

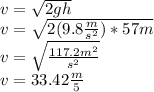
Have a great day