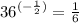Question

Which expression is equivalent to 36^-1/2

Answer 1

`36^{- (1)/(2) }= \cfrac{1}{36^{ (1)/(2) }} = \cfrac{1}{(6^2)^{ (1)/(2) }} = \cfrac{1}{6}`

Answer 2

ANSWER



`( {36})^{ (- (1)/(2)) } = (1)/(6)`


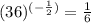
Step-by-step explanation



The given expression is



`{36}^{( - (1)/(2) )}`
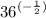
This is having a negative index. We must first of all change to a positive index.


Recall that,




`{a}^( - m) = \frac{1}{ {a}^(m) }`

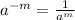
We apply this law of exponents to get,




`{36}^{( - (1)/(2) )} = \frac{1}{ {36}^{( (1)/(2) )} }`

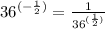
We cab rewrite the given expression to obtain;




`{36}^{( - (1)/(2) )} = (1)/( √(36) )`

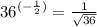
This will simplify to give us,



`{36}^{( - (1)/(2) )} = (1)/( 6 )`