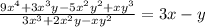Answer:
3x-y
Explanation:
- This is a polynomial of 4th order.
- To obtain the quotient, we use long division method
First step; in using long division method we look for a number which will multiply the first term of the denominator (divisor) to obtain exactly the first term of the numerator (dividend).
- In this question, First term of the divisor is 3x³
- First term of the numerator is 9x⁴
Hence, 3x³ multiply 3x = 9x⁴
Second step; multiply all the divisor by 3x and subtract the result from the dividend.
3x(3x³ + 2x²y - xy²) = 9x⁴ + 6x³y - 3x²y²
Subtract 9x⁴ + 6x³y - 3x²y² from 9x⁴ + 3x³y - 5x²y² + xy³
= 9x⁴ + 3x³y - 5x²y² + xy³ - (9x⁴ + 6x³y - 3x²y²)
= 9x⁴ + 3x³y - 5x²y² + xy³ - 9x⁴ - 6x³y +3x²y²
= -3x³y - 2x²y² + xy³ (this is the remainder after subtraction and becomes the new dividend)
Third step; note, the first term of the dividend has reduced to -3x³y, again think of a number that will multiply the first term of the divisor to obtain exactly -3x³y.
The number or term is '-y'; -y(3x³) = -3x³y
Fourth step; multiply all the divisor by -y and subtract the result from the dividend.
-y (3x³ + 2x²y - xy²) = -3x³y - 2x²y² + xy³
Subtract -3x³y - 2x²y² + xy³ from -3x³y - 2x²y² + xy³
= -3x³y - 2x²y² + xy³ - (-3x³y - 2x²y² + xy³)
= -3x³y - 2x²y² + xy³ +3x³y + 2x²y²- xy³
= 0
The remainder is now zero (0), we stop dividing
Note: All the terms used in multiplying the divisor before subtracting it from the dividend is the quotient of the long division.
HENCE,