Question

LM has endpoints L(-1 1) and M(-5 -3) find the coordinates of the midpoint of LM

Answer 1

Answer 2

Midpoint of LM is (-3-1).

Explanation:

LM has endpoints L(-11) and M(-5-3)

We have to find the coordinates of mid point of LM

If a line segment has two end points (x,y) and (x',y') then x-coordinates of the midpoint will be

x =
`(x+x')/(2)`

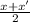
and y coordinates will be

Y =
`(y+y')/(2)`

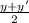
Now we put the values of endpoints to find midpoint of LM.

X =
`(-5-1)/(2)` =
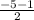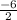`(-6)/(2)` = -3

Y =
`(1-3)/(2)` =
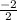`(-2)/(2)` = -1

Therefore, mid point of LM is (-3-1).