Question

. For the following true conditional statement, write the converse. If the converse is also true, combine the statements as a biconditional. If x = 8, then x2 = 64.

Answer 1

If
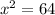`x^2=64`, then x=8

Explanation:

We are given that a conditional statement

If x=8, then
`x^2=64`

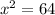
if conditional statement

`P\implies Q`

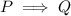
Then, converse statement

`Q\implies P`

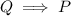
Converse statement of given conditional statement:

If
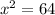`x^2=64`, then x=8

But , it is not true because when
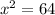`x^2=64`, then
`x=\pm 8`

Therefore, it is false.

Answer 2

Answer: The converse of the statement will be :

`\text{If }x^2 = 64\text{, then } x=8.` which is not true.

Explanation:

The given statement :
`\text{If } x = 8\text{, then }x^2 = 64.`

To write a converse of a conditional statement "p then q", will be "q then p" the hypothesis and conclusion interchanges .

Then the converse of the statement will be :

`\text{If } x^2 = 64\text{, then }x=8.` which is not true.

Since ,
`8^2=64\text{ and }-8^2=64`

Therefore,
`\text{If }x^2 = 64\text{, then } x=8\ or\ x=-8.`