Question

In a free-fall experiment, an object is dropped from a height of h = 400 feet. A camera on the ground 500 ft from the point of impact records the fall of the object (t

he shape is  a 90 degree angle with 500 ft at the bottom).


(a) Find the position function that yields the height of the object at time t assuming the object is released at time t = 0.
h(t) =


At what time will the object reach ground level? (Round your answer to three decimal places.)
t =
5.12
sec

(b) Find the rates of change of the angle of elevation of the camera when t = 1 and t = 2. (Round your answers to four decimal places.)
θ'(1) =
rad/sec
θ'(2) =
rad/sec

Answer 1

hmmm the object, is at rest, when dropped, so it has a velocity of 0 ft/s

the only force acting on the object, is gravity, using feet will then be -32ft/s²,


was wondering myself on -32 or 32.. but anyhow... we'll settle for the negative value, since it seems to be just a bit of convention issues

so, we'll do the integral to get v(t) then


`\bf \displaystyle \int -32\cdot dt\implies -32t+C \\\\\\ \textit{object moves from \underline{rest}, so velocity is 0 at 0secs} \\\\\\ -32(0)+C=0\implies C=0\implies \boxed{v(t)=-32t} \\\\\\ \textit{now to get the positional s(t)} \\\\\\ \displaystyle \int -32t\cdot dt\implies -16t^2+C \\\\\\ \textit{the initial \underline{position} was 400ft away at 0secs} \\\\\\ -16(0)^2+C=400\implies C=400\implies \boxed{s(t)=-16t^2+400}`

when will it reach the ground level? let's set s(t) = 0


`\bf s(t)=-16t^2+400\implies 0=-16t^2+400\implies \cfrac{-400}{-16}=t^2 \\\\\\ 25=t^2\implies \boxed{5=t}`


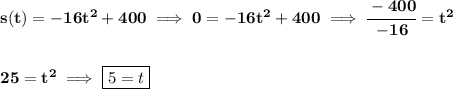
part B) check the picture below