Question

PLEASE HELPP

A quadratic function and an exponential function are graphed below. How do the decay rates of the functions compare over the interval
A
The exponential function decays at one-half the rate of the quadratic function.
B The exponential function decays at the same rate as the quadratic function.
C The exponential function decays at two-thirds the rate of the quadratic function.
D The exponential function decays at three-fourths the rate of the quadratic function.

Answer 1

D The exponential function decays at three-fourths the rate of the quadratic function.

Explanation:

We calculate the average slope of each graph in the indicated interval, the slope can be calculated as m=(y2-y1)/(x2-x1)

For the exponential function

`m_e=(4-1)/(-2-0)=-(3)/(2)`

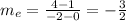
For the quadratic function

`m_q=(4-0)/(-2-0)=-(4)/(2)  =-2`

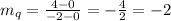
If we calculated de ratio of both average slopes:

`(m_e)/(m_q)=(-(3)/(2) )/(-2)  = (3)/(4)`

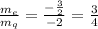
Therefore The exponential function decays at three-fourths the rate of the quadratic function.

Answer 2

The Decay rate for any function can be calculated by the formula Decay rate = [ difference in y values ÷difference in x values in given interval.].

Decay Rate for the exponential function in the interval -2≤x≤0. is (4-1)÷(-2-0)

= 3÷2.

Decay rate for quadratic function in same interval =[ (4-0)÷-(-2-0)] = 2÷1.

Ratio of decay rates=
`(3)/(2) :(2)/(1)=3:4.`

Option D The exponential function decays at three-fourths the rate of the quadratic function. is the right answer.