Question

PLEASEEE HELLPPP TIMED

A quadratic function and an exponential function are graphed below. How do the decay rates of the functions compare over the interval
A The exponential function decays at one-half the rate of the quadratic function.
B The exponential function decays at the same rate as the quadratic function.
C The exponential function decays at two-thirds the rate of the quadratic function.
D The exponential function decays at three-fourths the rate of the quadratic function.

Answer 1

The quadratic function decays by 4 units in the interval.
The exponential function decays by 3 units in the interval.

Thus,
D The exponential function decays at three-fourths the rate of the quadratic function.

Answer 2

Option: D is the correct answer.

D. The exponential function decays at three-fourths the rate of the quadratic function.

Explanation:

The graph of exponential function passes through (-2,4) and (0,1).

The rate of decay is given by:

`\text{Rate\ of\ decay}=|(1-4)/(0-(-2))|\\\\\\\text{Rate\ of\ decay}=|(-3)/(2)|\\\\\\\text{Rate\ of\ decay}=(3)/(2)`

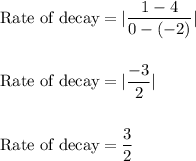
and the graph of quadratic function passes through (-2,4) and (0,0).

The rate of decay is given by:

`\text{Rate\ of\ decay}=|(0-4)/(0-(-2))|\\\\\\\text{Rate\ of\ decay}=|(-4)/(2)|\\\\\\\text{Rate\ of\ decay}=2`

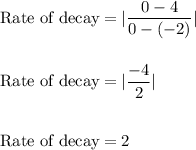
Hence, the rate of decay of exponential function decays at three-fourths the rate of the quadratic function.

( since,

`2* (3)/(4)=(3)/(2)`

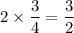
i.e.

rate of decay of quadratic function×(3/4)=Rate of decay of exponential function )