Question

Question 2 graphing please refering to question 1 letter b

Answer 1

Given the equation:

`9x^2-y^2=9`

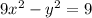
we can divide both sides by 9 to get the following:

`\begin{gathered} (1)/(9)(9x^2-y^2=9) \\ \\ \Rightarrow x^2-(y^2)/(9)=1 \\ (x^2)/(1)-(y^2)/(9)=1 \end{gathered}`

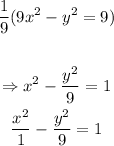
given the general equation of the hyperbola:

`(x^2)/(a^2)-(y^2)/(b^2)=1`

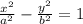
we have in this case that:

`\begin{gathered} a^2=1 \\ b^2=9 \\ \Rightarrow a=1 \\ b=3 \end{gathered}`

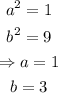
in this case, we have that the center is located at the origin, then:

`(h,k)=(0,0)`

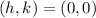
then, the vertices are:

`\begin{gathered} (h\pm a,0) \\ \Rightarrow(0\pm1,0) \\ \Rightarrow(1,0)^{} \\ \text{and} \\ (-1,0) \end{gathered}`

to find the focal points we have the following expression:

`\begin{gathered} (h\pm c,k) \\ \text{where:} \\ c=\sqrt[]{a^2+b^2} \end{gathered}`

then, we have:

`\begin{gathered} c=\sqrt[]{1+9}=\sqrt[]{10} \\ \Rightarrow(0\pm\sqrt[]{10},0) \\ \Rightarrow(\sqrt[]{10},0) \\ \text{and} \\ (-\sqrt[]{10},0) \end{gathered}`

to find the fundamental rectangle, we can find the corners with the following expressions:

`\begin{gathered} (0,b),(0,-b) \\ (a,0),,(-a,0) \\ \Rightarrow \\ (0,3),(0-3) \\ (1,0),(-1,0) \end{gathered}`

finally, we can find the asypmtotes with the folllowing equation:

`\begin{gathered} y=\pm(b)/(a)(x-h)+k \\ \Rightarrow y=\pm(3)/(1)(x-0)+0 \\ y=\pm3x \end{gathered}`

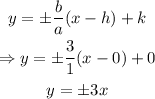
therefore, the graph of the hyperbola is: