Given the equation:
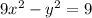
we can divide both sides by 9 to get the following:
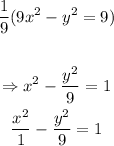
given the general equation of the hyperbola:
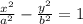
we have in this case that:
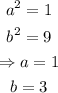
in this case, we have that the center is located at the origin, then:
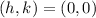
then, the vertices are:
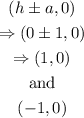
to find the focal points we have the following expression:
![\begin{gathered} (h\pm c,k) \\ \text{where:} \\ c=\sqrt[]{a^2+b^2} \end{gathered}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/high-school/kafiotuy0dogu5xaxcnf.png)
then, we have:
![\begin{gathered} c=\sqrt[]{1+9}=\sqrt[]{10} \\ \Rightarrow(0\pm\sqrt[]{10},0) \\ \Rightarrow(\sqrt[]{10},0) \\ \text{and} \\ (-\sqrt[]{10},0) \end{gathered}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/high-school/2phro143unkiuyzl4d18.png)
to find the fundamental rectangle, we can find the corners with the following expressions:
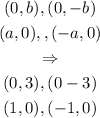
finally, we can find the asypmtotes with the folllowing equation:
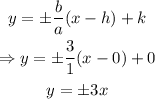
therefore, the graph of the hyperbola is: