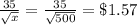Given that a fabrics company finds that the cost and revenue, in dollars, of producing x jackets is given by
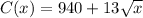
and

respectively.
The profit of the company from producing x jackets is given by P(x) = R(x) - C(x) =
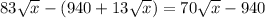
The rate at which the fabric company's average profit per jacket is changing is given by
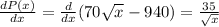
Therefore, the
the rate at which the fabric company's average profit per jacket is changing when 500 jackets have been produced and sold is given by