Question

PLEASEE HELP ANYONE

Which graph has a rate of change equal to 1/3  in the interval between 0 and 3 on the x-axis?

Answer 1

Rate of change is like slope between the two points. The x values given are 0 and 3. Starting st the first option we find the matching y values and the find the slope.
Option 1: (0, 2) (3, 4)
m = (4-2)/(3-0) = 2/3 No
Option 2: (0, 0) (3, 6)
m = (6-0)/(3-0) = 6/3=2 No
Option 3: (0, 1.5) (3,2.5)
m = (2.5-1.5)/(3-0) = 1/3 Yes
Option 4: (0,1) (3, 0)
m = (0-1)/(3-0) =-1/3 No
Only Option 3

Answer 2

Answer: The correct option is the THIRD GRAPH. Its image is attached below.

Step-by-step explanation: We are given to select the graph that has a rate of change equal to
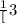`\frac{1}[3}` in the interval between 0 and 3 on the X-axis.

We know that

the rate of change of a function f(x) in the interval x = a to x = b is given by

`R_c=(f(b)-f(a))/(b-a).`

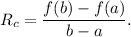
FIRST GRAPH :

Here the value of the function at the points x = 0 and x = 3 are given by

`f(0)=2,~~f(3)=4.`

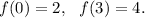
So, the rate of change in the interval [0, 3] will be

`R_c=(f(3)-f(0))/(3-0)=(4-2)/(3-0)=(2)/(3)\\eq (1)/(3).`

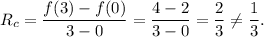
This option is NOT correct.

SECOND GRAPH :

Here the value of the function at the points x = 0 and x = 3 are given by

`f(0)=0,~~f(3)=6.`

So, the rate of change in the interval [0, 3] will be

`R_c=(f(3)-f(0))/(3-0)=(6-0)/(3-0)=(6)/(3)=2\\eq (1)/(3).`

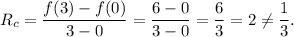
This option is NOT correct.

THIRD GRAPH :

Here the value of the function at the points x = 0 and x = 3 are given by

`f(0)=(3)/(2),~~f(3)=(5)/(2).`

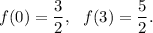
So, the rate of change in the interval [0, 3] will be

`R_c=(f(3)-f(0))/(3-0)=((5)/(2)-(3)/(2))/(3-0)=(2)/(2*3)=(1)/(3).`

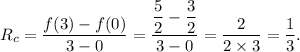
This option is CORRECT.

FOURTH GRAPH :

Here the value of the function at the points x = 0 and x = 3 are given by

`f(0)=(1)/(2),~~f(3)=0.`

So, the rate of change in the interval [0, 3] will be

`R_c=(f(3)-f(0))/(3-0)=(0-(1)/(2))/(3-0)=-(1)/(6)\\eq (1)/(3).`

This option is NOT correct.

Thus, the correct option is the THIRD GRAPH. Its image is attached below.