Question

What value is a discontinuity of x squared plus 5 x plus 2, all over x squared plus 2 x minus 35?

Answer 1

The value of discontinuity is x= -7, x= 5

Answer 2

x=-7 and x=5.

Step-by-step explanation:

We have been given a rational function:
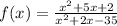`f(x)=(x^2+5x+2)/(x^2+2x-35)`. We are asked to find the points at which our function is discontinuous.

A rational function is discontinuous when the function is undefined or the denominator is zero.

Let us find what values of x will make our denominator zero.

`x^2+2x-35=0`

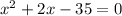
We will use factoring to find the zeros of x. By splitting the middle term we will get,

`x^2+7x-5x-35=0`

`x(x+7)-5(x+7)=0`

`(x+7)(x-5)=0`

`(x+7)=0\text{ or }(x-5)=0`

`x=-7\text{ or }x=5`

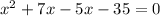
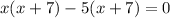
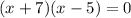
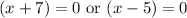
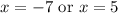
Therefore, at x equals -7 and x equals 5 our function is discontinuous.