Question

How many grams of iron metal do you expect to be produced when 245 grams of an 80.5 percent by mass iron (II) nitrate solution react with excess aluminum metal? Show all of the work needed to solve this problem. 2Al (s) + 3Fe(NO3)2 (aq) yields 3Fe (s) + 2Al(NO3)3 (aq)

Answer 1

2Al + 3Fe(NO₃)₂ = 3Fe + 2Al(NO₃)₃

m=245 g
w=0.805 (80.5%)
M{Fe(NO₃)₂}=179.857 g/mol
M(Fe)=55.847 g/mol

1. the mass of salt in solution is:
m{Fe(NO₃)₂}=mw

2. the proportion follows from the equation of reaction:
m(Fe)/3M(Fe)=m{Fe(NO₃)₂}/3M{Fe(NO₃)₂}

m(Fe)=M(Fe)m{Fe(NO₃)₂}/M{Fe(NO₃)₂}

m(Fe)=M(Fe)mw/M{Fe(NO₃)₂}

m(Fe)=55.847*245*0.805/179.857= 61.24 g

Answer 2

Answer : The mass of iron metal produced will be, 61.376 grams.

Solution : Given,

Molar mass of iron(II)nitrate = 179.85 g/mole

Molar mass of Fe = 56 g/mole

First we have to calculate the mass of iron(II)nitrate.

`\text{Mass of }Fe(NO_3)_2=(80.5)/(100)* 245=197.225g`

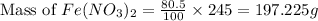
Now we have to calculate the moles of iron(II)nitrate.

`\text{Moles of }Fe(NO_3)_2=\frac{\text{Mass of }Fe(NO_3)_2}{\text{Molar mass of }Fe(NO_3)_2}=(197.225g)/(179.85g/mole)=1.096moles`

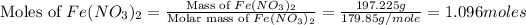
Now we have to calculate the moles of iron metal.

The given balanced reaction is,

`2Al(s)+3Fe(NO_3)_2(aq)\rightarrow 3Fe(s)+2Al(NO_3)_3(aq)`

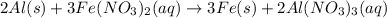
From the balanced reaction, we conclude that

As, 3 moles of iron(II)nitrate react to give 3 moles of iron metal

So, 1.096 moles of iron(II)nitrate react to give
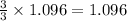`(3)/(3)* 1.096=1.096` moles of iron metal

Now we have to calculate the mass of iron metal.

`\text{Mass of }Fe=\text{Moles of }Fe* \text{Molar mass of }Fe`

`\text{Mass of }Fe=(1.096mole)* (56g/mole)=61.376g`

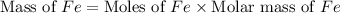
Therefore, the mass of iron metal produced will be, 61.376 grams.