Question

Which polynomial is the correct product? (2y+3)(3y2+4y+5)

Answer 1

(2y+3)(3(y^2)+4y+5)
(2y)(3(y^2))+(2y(4y))+(2y)(5)+(3(3)(y^2))+(3)(4y)+(3)(5)
6(y^3)+8(y^2)+10y+9(y^2)+12y+15
6(y^3)+17(y^2)+22y+15

Answer 2

`6y^(3)+17y^2+22y+15`

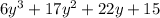
Explanation:

We are asked to find the polynomial that is the result of the product of
`(2y+3)(3y^2+4y+5)`.

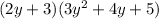We will use distributive property
`a(b+c)=a*b+a*c` to solve our given problem.

`2y(3y^2+4y+5)+3(3y^2+4y+5)`

`2y*3y^2+2y*4y+2y*5+3*3y^2+3*4y+3*5`

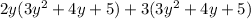
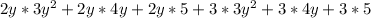
We will use exponent property
`a^m\cdot a^n =a^(m+n)` to simplify our polynomial.

`2*3y^(2+1)+2*4y^(1+1)+2y*5+3*3y^2+3*4y+3*5`

`6y^(3)+8y^(2)+10y+9y^2+12y+15`

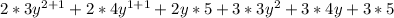
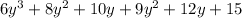
Now we will combine like terms.

`6y^(3)+8y^(2)+9y^2+12y+10y+15`

`6y^(3)+17y^2+22y+15`

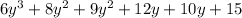
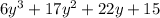
Therefore, the polynomial
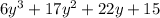`6y^(3)+17y^2+22y+15` is the correct product of our given expressions.