Answer:
x = 4
 y = 7 and z =3
y = 7 and z =3

This implies the equation has just one solution
Explanation:
To create the equation, we need to be able to write the information or interpret the question mathematically.
Let x equal to the number of red balls.
Let y equal to the number of blue balls.
Let z equal to the number of green balls.
From the question; "The number of red balls is 2/3 the number of blue balls" can be mathematically written as : x =
 y ---------------------------(1)
y ---------------------------(1)
The next statement; "The number of green balls is 1 more than 1/3 the number of blue balls" can be written mathematically as: z = 1+
 y ----------------------------(2)
y ----------------------------(2)
The next statement; "she has 15 balls." can be mathematically written as: x + y + z = 15 ----------------------------------------(3)
Substitute equation (1) and equation (2) into equation (3)
 y + y +1 +
y + y +1 +
 y = 15
y = 15
We can rearrange this equation
 y +
y +
 y + y +1 = 15
y + y +1 = 15
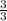 y + y + 1 = 15
y + y + 1 = 15
y + y + 1 = 15
2y + 1 = 15
subtract 1 from both-side of the equation
2y + 1 -1 = 15 -1
2y = 14
Divide both-side of the equation by 2
2y/2 = 14/2
y = 7
Substitute y = 7 into equation (1)
x =
 y
y
x =
 (7)
(7)
x = 14/3
x = 4

Substitute y= 7 in equation (2)
z = 1+
 y
y
z = 1+
 (7)
(7)
z = 1+ 7/3
z = 10/3
z =3

Therefore;
x = 4
 y = 7 and z =3
y = 7 and z =3

This implies the equation has just one solution.