The Solution:
Given:
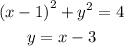
Required:
To determine all the points where the graphs of the two equations intersect.
Below is the graph of the two equations:
Clearly, we can see from the graph that the points the two equations intersect are:
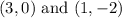
Therefore, the correct answers are [options C and E]