Answer:
Answer is 6
Explanation:
Given that there is an arithmetic sequence and has an explicit formula for the nth term as
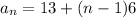
Since n can be any natural number, let us substitute n =1 to find the I term
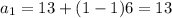
Let us find the 2nd term by substituting n=2
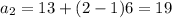
Common difference = d=
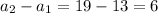
Hence from I term a and common difference d, we find the any term can be obtained by adding 6 to the previous term
i.e.
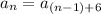
6 is the answer