Question

Given the equations 9x+3/4y=6 and 2x+1/2y=9, by what factor the equation to eliminate y and solve the system through linea would you multiply the second equation to eliminate y and solve the system through linear combinations?

Options;
A.) -4/3
B.) -3/4
C.) -3/2
D.) -7/2

Answer 1

C -3/2

Just multiply the second equation by -3/2
this will make the y term = -3/4y

so adding will eliminate the y terms.

Answer 2

`-(3)/(2)`

C is correct.

Explanation:

Given: System of equation

`9x+(3)/(4)y=6`

`2x+(1)/(2)y=9`

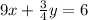
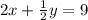
We have to solve system of equation by eliminating y

So, first we will make the coefficient of y same with opposite sign.

Coefficient of y in first equation 3/4

Coefficient of y in 2nd equation 1/2

`LCM \ of\ (3)/(4)\ and\ (1)/(2)=(3)/(2)`

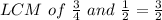
Multiply second equation by -3/2 to make coefficient of y same

`-(3)/(2)\cdot 2x-(3)/(2)\cdot (1)/(2)y=-(3)/(2)\cdot 9`

`-3x-(3)/(4)y=-(27)/(2)`

`9x+(3)/(4)y=6`

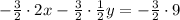
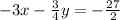
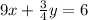
Add both equation and eliminate y

`-3x+9x=-(27)/(2)+6`

`6x=-(15)/(2)`

`x=-(5)/(4)`

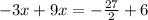
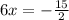
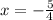
Hence, We multiply by -3/2 to eliminate y and solve the system of equation.