Question

3.Solve the system of equations by forming a matrix equation. Solve by multiplying each side of the system of equations by the inverse matrix. Show computation of the inverse matrix by showing the calculation of the determinant. State your answer as an ordered pair. x+5 = - 14-2x-5y = 23

Answer 1

We want to solve the simultaneous equation

`\begin{gathered} x+5=-14 \\ -2x-5y=23 \end{gathered}`

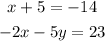
We will rearrage this to become

`\begin{gathered} x+0y=-19 \\ -2x-5y=23 \end{gathered}`

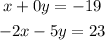
Writing this as a matrix equation, we get

`\begin{bmatrix}{1} & {0} & {} \\ {-2} & {-5} & \end{bmatrix}\begin{bmatrix}{x} & {} \\ {y} & \end{bmatrix}=\begin{bmatrix}{-19} & {} \\ {23} & \end{bmatrix}`

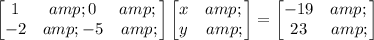
From the above matrix equation we will take

`\begin{gathered} A=\begin{bmatrix}{1} & {0} & {} \\ {-2} & {-5} & \end{bmatrix} \\ B=\begin{bmatrix}{x} & {} \\ {y} & \end{bmatrix} \\ C=\begin{bmatrix}{-19} & {} \\ {23} & \end{bmatrix} \end{gathered}`

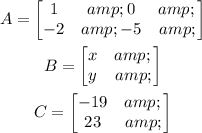
So, this means that

`\begin{gathered} A* B=C \\ AB=C \\ B=(C)/(A) \\ B=C* A^(-1) \\ B=CA^(-1) \end{gathered}`

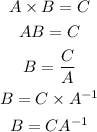
Now, we have to find the inverse matrix, which is

`A^(-1)`

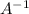
This is given as

`\begin{gathered} A^(-1)=(1)/(|A|)* Adj\text{ A} \\ A^(-1)=(1)/(ad-bc)*\begin{bmatrix}{d} & {-b} & {} \\ {-c} & {a} & \end{bmatrix} \end{gathered}`

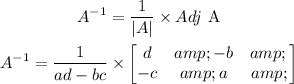
So, if we have

`\begin{bmatrix}{a} & {b} & {} \\ {c} & {d} & \end{bmatrix}=\begin{bmatrix}{1} & {0} & {} \\ {-2} & {-5} & \end{bmatrix}`

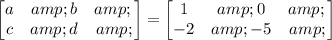
Then

`\begin{gathered} A^(-1)=(1)/(ad-bc)*\begin{bmatrix}{d} & {-b} & {} \\ {-c} & {a} & \end{bmatrix} \\ A^(-1)=(1)/(1(-5)-0(-2))*\begin{bmatrix}{-5} & {0} & {} \\ {2} & {1} & \end{bmatrix} \\ A^(-1)=(1)/(-5)\begin{bmatrix}{-5} & {0} & {} \\ {2} & {1} & \end{bmatrix} \end{gathered}`

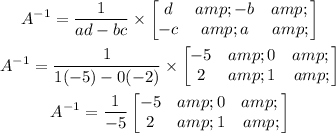
Hence, the inverse matrix is

`A^(-1)=(1)/(-5)\begin{bmatrix}{-5} & {0} & {} \\ {2} & {1} & \end{bmatrix}`

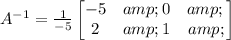
Now, from

`B=CA^(-1)`

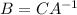
We will have

`\begin{gathered} \begin{bmatrix}{x} & {} \\ {y} & \end{bmatrix}=(1)/(-5)\begin{bmatrix}{-5} & {0} & {} \\ {2} & {1} & \end{bmatrix}\begin{bmatrix}{-19} & {} \\ {23} & \end{bmatrix} \\ \begin{bmatrix}{x} & {} \\ {y} & \end{bmatrix}=(1)/(-5)\begin{bmatrix}{95} & {} \\ {-38+23} & \end{bmatrix} \\ \begin{bmatrix}{x} & {} \\ {y} & \end{bmatrix}=(1)/(-5)\begin{bmatrix}{95} & {} \\ {-15} & \end{bmatrix} \\ \begin{bmatrix}{x} & {} \\ {y} & \end{bmatrix}=\begin{bmatrix}{-19} & {} \\ {3} & \end{bmatrix} \end{gathered}`

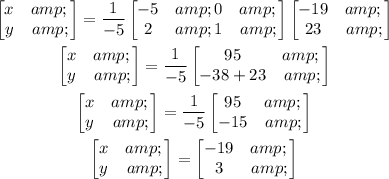
Hence from the matrix,

x = -19 and y = 3